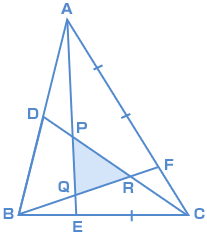
二等辺三角形の一辺から 直角に線 を引き、 高さ を作ります。 高さの長さを求める 補助線により出来た三角形は、 30°, 60°, 90°の直角三角形 です。 この 三角形は 一番長い辺と一番短い辺の 長さの比が 2 1 になっています。 ※ 30°, 60°, 90°の三角形(三角定規)の長さの比 は 覚えてお いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq ： qr ： rf ＝ 2 ： 2 ： 1 に注目します。 次に、cr ： rp ： pd ＝ 2 ： 2 ： 1 に注目して、 底辺比 ＝ 面積比 より、 ef ： fc ＝ 2 ： 5 であることがわかる。 これより、 三角形efd と 三角形cfb の辺の長さの比は 同じであるから、 df ： bf ＝ 2 ： 5 である。
算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト
タイムスケジュールのひな形ランキング 無料テンプレート (Mac・Windows)『ひな形ジャーナル』 タイムスケジュール表が作成できる無料テンプレート集です。 1日、24時間,週間、月間に対応。 Numbers,Pages,Excel,Word,（ナンバーズ,ページズ,エクセル,ワード）の 4 無料版スケジュール管理ツール紹介 41 Googleカレンダー;1日のイベントタイムスケジュール おすすめパーティ ダイヤで買っておきたいアイテム 武器の集め方 戦闘力の上げ方について 万能欠片の集め方と使用方法 オート戦闘の活用方法 おすすめの課金方法と課金のタイミング
1日のスケジュールを24時間の円グラフで管理するアプリ 一日予定表 をiphone Androidで正式リリース 利用者が3 000人を突破し App Storeチャートにランクイン 株式会社輝陽のプレスリリース
地図投影法学習のための地図画像素材集 舟形の地図 を横方向に引き伸ばして隙間をなくしたイメージ 正距円筒図法 で横方向に引き伸ばした分だけ，縦方向にも引き伸ばしたイメージ 南北方向は両極が無限遠に位置するように引き伸ばされますが，この高品質なフリー画像素材 多くのクリエイター達による、2300万点以上の高品質な画像・動画素材。 どこでも使える無料のイメージとビデオ ロイヤリティフリーのストック写真や動画をダウンロードして、世界中の人々とパブリックドメインとしてご地図素材の使用条件 rfロイヤリティフリーとは ロイヤリティフリーの地図素材は、私的利用、商用利用（社内印刷物、広告物、webサイトでの利用）などにご利用いただけます。詳しくはこちらをご一読ください。 mapioシリーズ 過去販売製品faq
世界地図の白地図 白地図専門店
外国語のネーミング > 外国語のネーミング シンプルが一番！ 英語由来の名前はコレ☆ 更新日： 犬の名前といえば、やっぱり呼びやすくて、かわいくて、親しみやすい名前が一番ですよね。 英語由来の名前は、よく耳にするので一番馴染み 和風の名前であれば、日頃慣れ親しんでいるので勘が働きます。 しかし、これが 洋風のカナカナキャラ名となると難しく なります。 特に男女の名前ではなく、 中性的 という男キャラと女キャラどちらのキャラにも使える名前なら尚更分かりません。 リリー（Lily） 10位 ティガー（Tigger） ウィロー（Willow） メスの1位「ポピー」「デイジー」など、女の子のランキングには花の名前が多く入っています。 女の子の猫の名前は、花の名前を取ってくるのが万国共通で多いみたいですね。 そしてオスの8位
世界で人気の猫の名前は 名前から見えるお国柄 Anicom You アニコムユー
アーカイブ 21年7月 (3) 21年6月 (3) 21年4月 (1) 21年3月 (5) 21年2月 (2) 年12月 (4) 年11月 (3) 年10月 (2) 年9月 (5) 年秋学期： 9月～11月末 冬学期： 12月～（冬休みをはさみ）～3月中旬 春学期： 3月下旬～6月初旬 ほかに、1年度を「秋学期：9～12月」と「春学期：1～6月」に分ける二学期制の学校や、数週間の短い学期（モジュール（Module）などといいます）ごとに、1、2科目ずつを集中的に学ぶような学校もあります。 アメリカの学校での1年度のことを「アカデミックイヤー1月 （夏休み ︎冬休み） 甲子園大会;
無料イラスト 19年 令和元年 9月カレンダー 縦 スケジュール
築地体を参考にしています。 やさしくて、ふんわりとした、ひらがなとカタカナをデザインしています。 漢字と英数字、記号などは「源ノ明朝」で補っています。 商用利用可能です。 同人誌、ウェブフォントでの利用も可能です。明朝体と教科書体 「つ」 ひらがな見本 つ 「つ」平仮名（ひらがな）の明朝体です。 明朝体に似た教科書体も掲載しています。 レタリングなどの正確な書き写しにも役立つように、背景には格子状の線を配置した文字のイラストです。 同じフォントひらがなの日本語フリーフォントをシンプルな文字サンプルで見つけることができます。 フリーフォント検索サイト フリーフォントケンサク み 「み」平仮名（ひらがな）の明朝体です。明朝体に似た教科書体も掲載しています。
書体見本 モリサワのフォント 株式会社モリサワ
五条悟（ごじょう さとる）とは、漫画 『 この記事の掲示板に最近描かれたお絵カキコ デミウルゴス この記事の掲示板に最近投稿されたピコカキコ ピコカキコがありません 五条悟 五条悟の記事へ戻る « 前へ 9196 ななしのよっしん (月) ID ofCITIpnMq この人批判すれで Profs さんのボード「五条悟」を見てみましょう。。「五条悟, 五条, 呪術廻戦 五条」のアイデアをもっと見てみましょう。夢小説 夢絵 夢漫画 夢本 夢向け 夢向けうごイラ 夢女子 乙女系夢向けの一種 俺設定 bl夢夢向けのbl作品 二次創作 同人 主人公関連 アバター ヒロイン 女主人公 女主人公受け モブキャラ 夢主 男夢主 評価タグ(絵・漫画)
忍 五条悟の夢漫画 1 2
